This Distribution Occurs Over and Over Again With Many Different Types of Data

The Poisson Distribution and Poisson Process Explained
A straightforward walk-through of a useful statistical concept
A tragedy of statistics in most schools is how boring it's fabricated. Teachers spend hours wading through derivations, equations, and theorems, and, when you finally get to the best part — applying concepts to actual numbers — information technology's with irrelevant, unimaginative examples like rolling dice. This is a shame every bit stats can exist enjoyable if you lot skip the derivations (which you'll likely never demand) and focus on using the ideas to solve interesting problems.
In this article, we'll cover Poisson Processes and the Poisson distribution, two important probability concepts. Later highlighting just the relevant theory, we'll piece of work through a existent-world instance, showing equations and graphs to put the ideas in a proper context.
Poisson Procedure
A Poisson Procedure is a model for a series of discrete consequence where the average fourth dimension between events is known, only the exact timing of events is random. The inflow of an effect is independent of the event before (waiting time between events is memoryless). For instance, suppose we ain a website which our content delivery network (CDN) tells u.s. goes downwards on boilerplate once per threescore days, only i failure doesn't affect the probability of the side by side. All we know is the average time between failures. This is a Poisson process that looks similar:
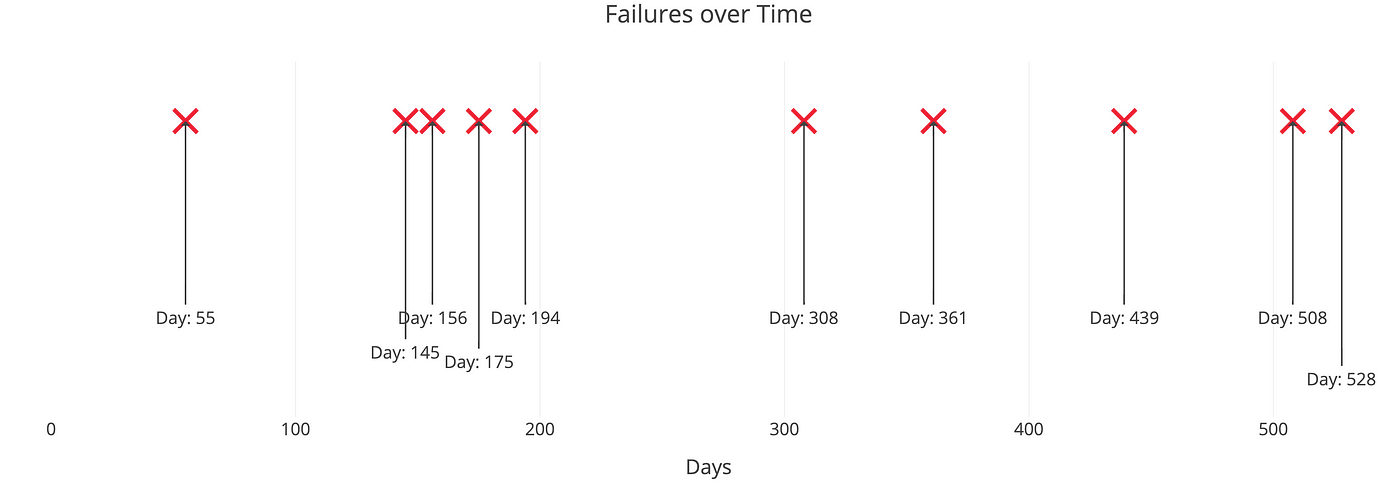
The important indicate is nosotros know the average time between events but they are randomly spaced (stochastic). We might have back-to-dorsum failures, but we could also go years betwixt failures due to the randomness of the process.
A Poisson Procedure meets the following criteria (in reality many phenomena modeled as Poisson processes don't come across these exactly):
- Events are independent of each other. The occurrence of ane upshot does not bear upon the probability another result will occur.
- The average charge per unit (events per time period) is abiding.
- Two events cannot occur at the same time.
The last point — events are not simultaneous — means we can think of each sub-interval of a Poisson procedure every bit a Bernoulli Trial, that is, either a success or a failure. With our website, the entire interval may be 600 days, only each sub-interval — one day — our website either goes down or information technology doesn't.
Mutual examples of Poisson processes are customers calling a help heart, visitors to a website, radioactive decay in atoms, photons arriving at a space telescope, and movements in a stock price. Poisson processes are by and large associated with time, merely they do not accept to be. In the stock case, nosotros might know the average movements per twenty-four hours (events per time), but we could too take a Poisson process for the number of trees in an acre (events per area).
(One instance frequently given for a Poisson Process is bus arrivals (or trains or now Ubers). However, this is not a true Poisson procedure because the arrivals are non independent of one some other. Even for bus systems that do not run on fourth dimension, whether or not one motorcoach is tardily affects the arrival time of the next bus. Jake VanderPlas has a bang-up article on applying a Poisson process to jitney arrival times which works better with made-up data than existent-globe data.)
Poisson Distribution
The Poisson Process is the model we apply for describing randomly occurring events and by itself, isn't that useful. We need the Poisson Distribution to practise interesting things similar finding the probability of a number of events in a time period or finding the probability of waiting some time until the side by side event.
The Poisson Distribution probability mass function gives the probability of observing k events in a time period given the length of the period and the average events per time:
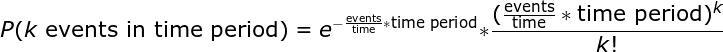
This is a little convoluted, and events/time * time period is usually simplified into a unmarried parameter, λ, lambda, the charge per unit parameter. With this substitution, the Poisson Distribution probability office now has one parameter:

Lambda can exist thought of as the expected number of events in the interval. (Nosotros'll switch to calling this an interval because remember, we don't accept to utilise a time period, nosotros could use area or volume based on our Poisson process). I like to write out lambda to remind myself the charge per unit parameter is a role of both the average events per time and the length of the time flow but you'll near commonly see information technology as directly above.
As nosotros change the rate parameter, λ, nosotros change the probability of seeing different numbers of events in one interval. The below graph is the probability mass function of the Poisson distribution showing the probability of a number of events occurring in an interval with dissimilar rate parameters.
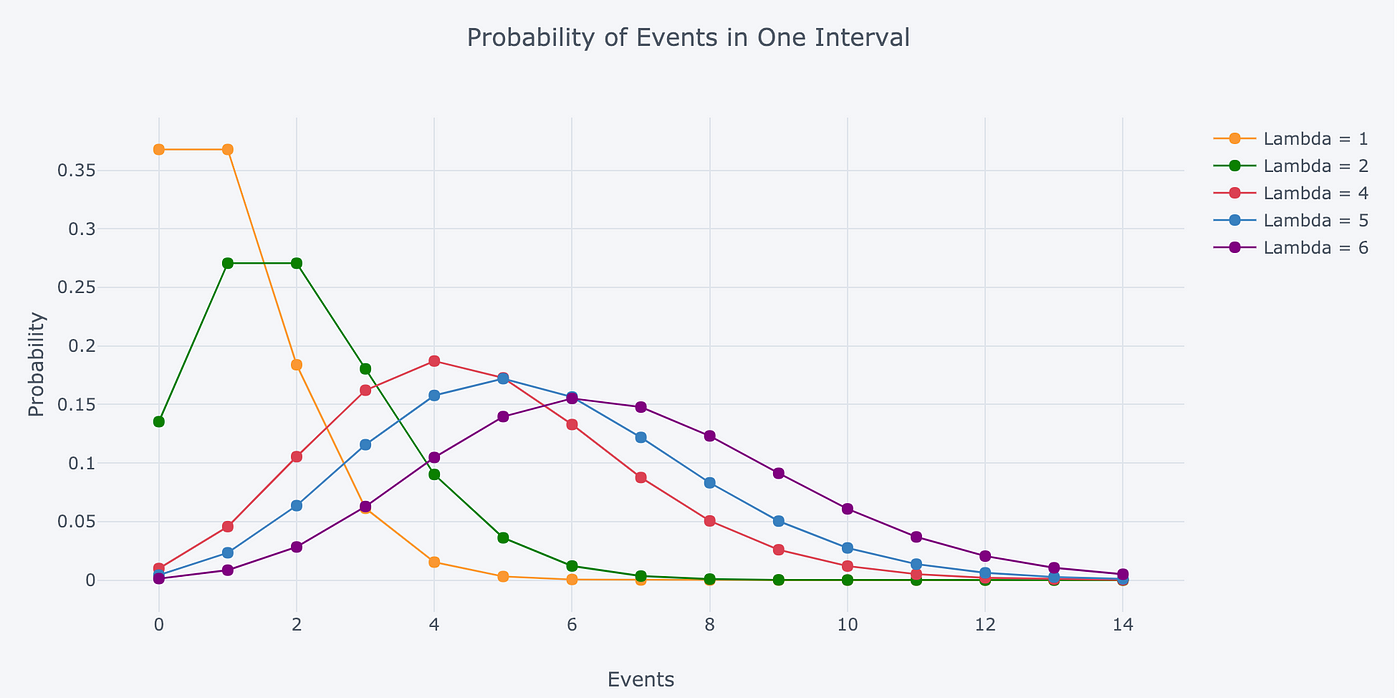
The most likely number of events in the interval for each curve is the charge per unit parameter. This makes sense considering the rate parameter is the expected number of events in the interval and therefore when it'southward an integer, the rate parameter will exist the number of events with the greatest probability.
When it's not an integer, the highest probability number of events will be the nearest integer to the rate parameter, since the Poisson distribution is just defined for a discrete number of events. The detached nature of the Poisson distribution is besides why this is a probability mass function and not a density function. (The rate parameter is also the mean and variance of the distribution, which exercise not need to exist integers.)
We can use the Poisson Distribution mass role to find the probability of observing a number of events over an interval generated past a Poisson process. Another use of the mass function equation — as we'll run into subsequently — is to find the probability of waiting some time between events.
A Worked-Out Example
For the problem nosotros'll solve with a Poisson distribution, nosotros could continue with website failures, but I propose something grander. In my childhood, my father would often take me into our yard to observe (or try to detect) meteor showers. Nosotros were not space geeks, simply watching objects from outer space burn up in the sky was plenty to go u.s. outside even though falling star showers e'er seemed to occur in the coldest months.
The number of meteors seen tin be modeled as a Poisson distribution because the meteors are independent, the average number of meteors per hour is constant (in the short term), and — this is an approximation — meteors don't occur simultaneously. To characterize the Poisson distribution, all we need is the rate parameter which is the number of events/interval * interval length. From what I remember, we were told to expect v meteors per hour on average or 1 every 12 minutes. Due to the limited patience of a immature child (especially on a freezing night), nosotros never stayed out more than hour, and then we'll utilize that as the time catamenia. Putting the two together, nosotros become:
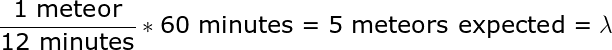
What exactly does "5 meteors expected" mean? Well, co-ordinate to my pessimistic dad, that meant we'd see three meteors in an hour, tops. At the time, I had no data science skills and trusted his judgment. Now that I'g older and take a good for you corporeality of skepticism towards authority figures, it's time to put his statement to the test. We can utilise the Poisson distribution to discover the probability of seeing exactly 3 meteors in one hour of observation:
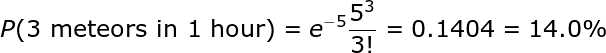
14% or most ane/7. If we went outside every nighttime for ane week, so nosotros could expect my dad to exist right precisely one time! While that is nice to know, what we are after is the distribution, the probability of seeing unlike numbers of meteors. Doing this by hand is tedious, so we'll use Python — which you tin encounter in this Jupyter Notebook — for calculation and visualization.
The below graph shows the Probability Mass Function for the number of meteors in an hour with an boilerplate fourth dimension between meteors of 12 minutes (which is the aforementioned as saying 5 meteors expected in an hr).
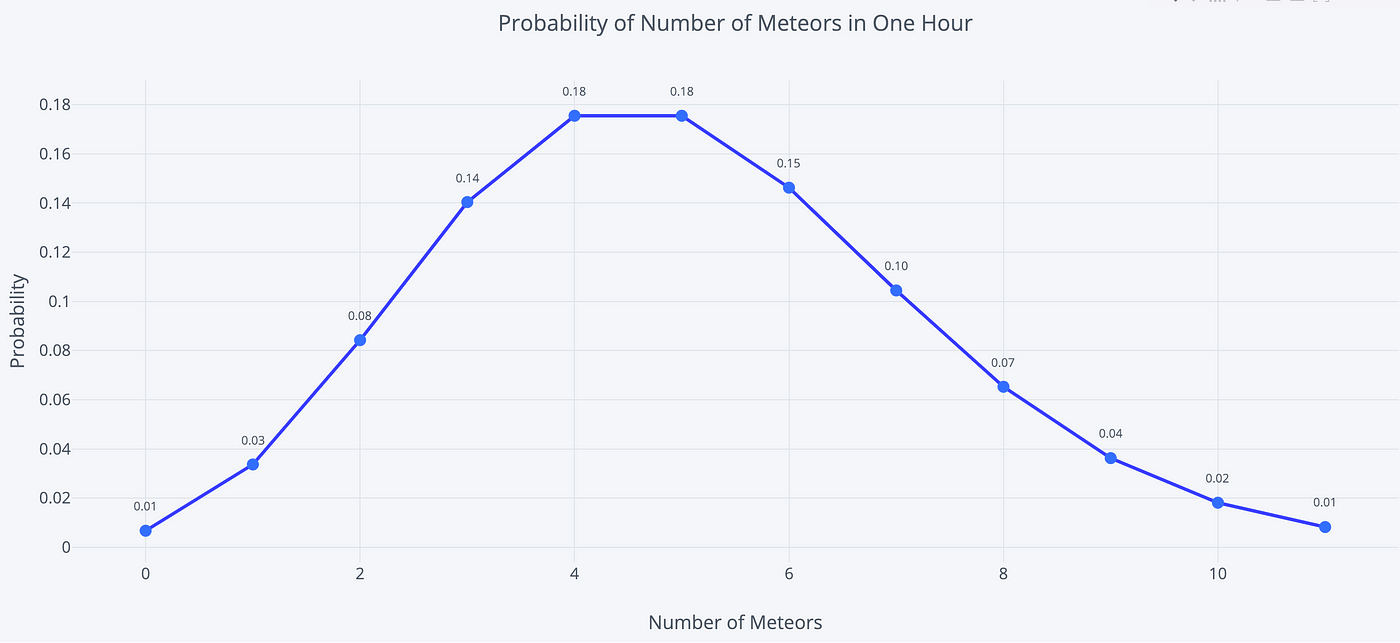
This is what "5 expected events" means! The near probable number of meteors is 5, the rate parameter of the distribution. (Due to a quirk of the numbers, 4 and 5 have the aforementioned probability, 18%). Equally with whatever distribution, there is 1 nearly likely value, but there are also a wide range of possible values. For instance, we could go out and run across 0 meteors, or we could see more than ten in one 60 minutes. To find the probabilities of these events, nosotros utilise the aforementioned equation but this time summate sums of probabilities (see notebook for details).
We already calculated the chance of seeing exactly 3 meteors equally about 14%. The hazard of seeing 3 or fewer meteors in one hour is 27% which means the probability of seeing more 3 is 73%. Likewise, the probability of more than 5 meteors is 38.4% while we could expect to see 5 or fewer meteors in 61.6% of observation hours. Although information technology's small, there is a 1.4% chance of observing more 10 meteors in an hour!
To visualize these possible scenarios, we tin run an experiment past having our sister record the number of meteors she sees every hour for 10,000 hours. The results are shown in the histogram below:
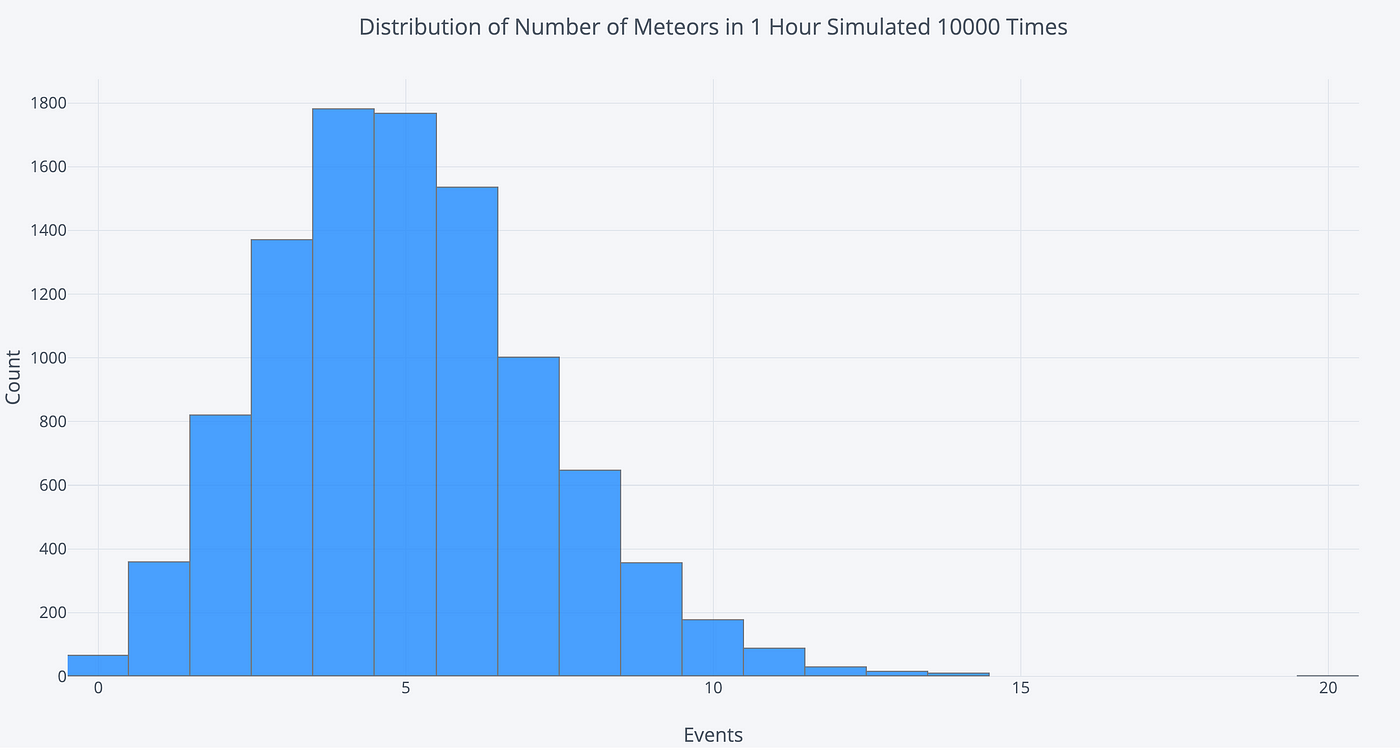
(This is obviously a simulation. No sisters were employed for this article.) Looking at the possible outcomes reinforces that this is a distribution and the expected result does non always occur. On a few lucky nights, we'd witness 10 or more meteors in an hour, although we'd usually see four or 5 meteors.
Experimenting with the Charge per unit Parameter
The rate parameter, λ, is the simply number we demand to define the Poisson distribution. Withal, since information technology is a product of two parts (events/interval * interval length) there are 2 means to modify it: nosotros can increase or decrease the events/interval and we tin increase or decrease the interval length.
Outset, allow's change the rate parameter by increasing or decreasing the number of meteors per hour to see how the distribution is afflicted. For this graph, we are keeping the fourth dimension menses constant at hour (1 hour).
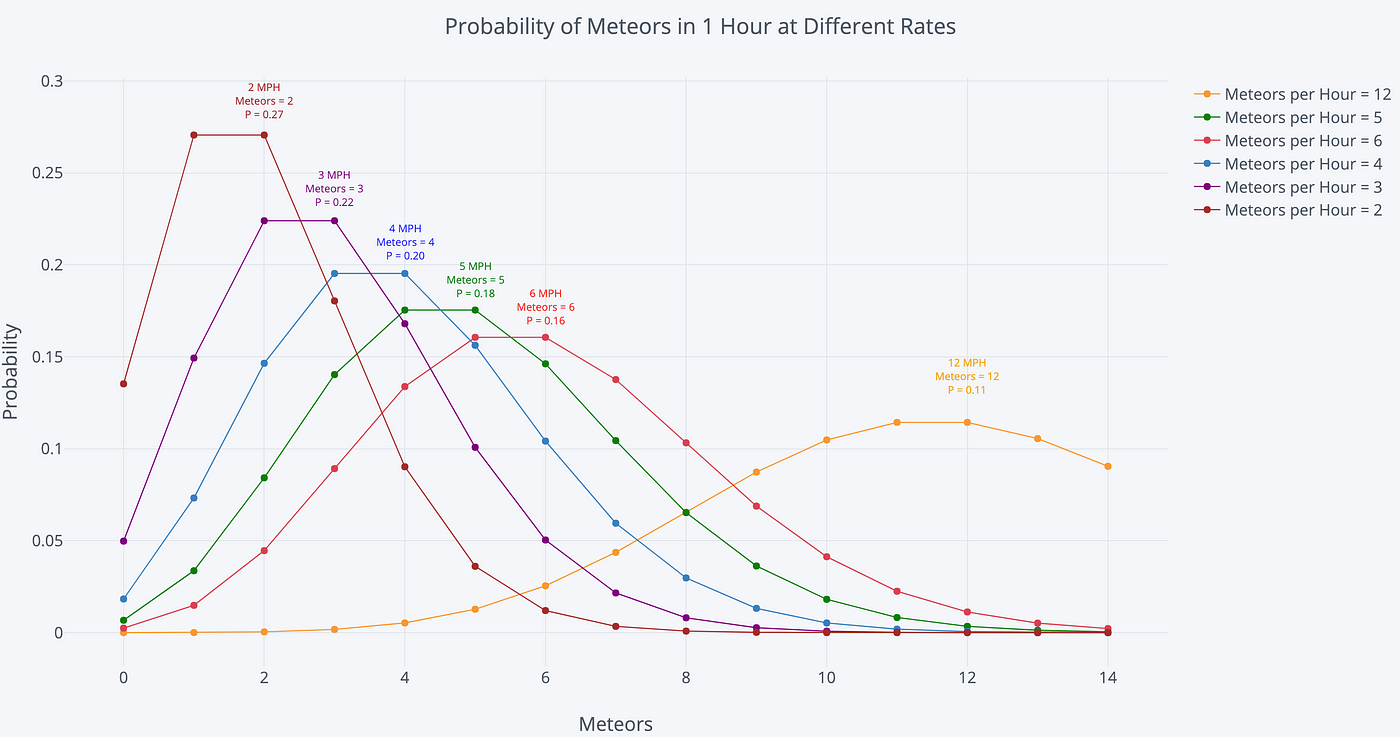
In each case, the most probable number of meteors over the 60 minutes is the expected number of meteors, the rate parameter for the Poisson distribution. As one example, at 12 meteors per hour (MPH), our rate parameter is 12 and there is an 11% take a chance of observing exactly 12 meteors in 1 60 minutes. If our rate parameter increases, we should expect to see more meteors per hour.
Another option is to increment or decrease the interval length. Below is the same plot, but this time we are keeping the number of meteors per hour constant at 5 and irresolute the length of fourth dimension we observe.
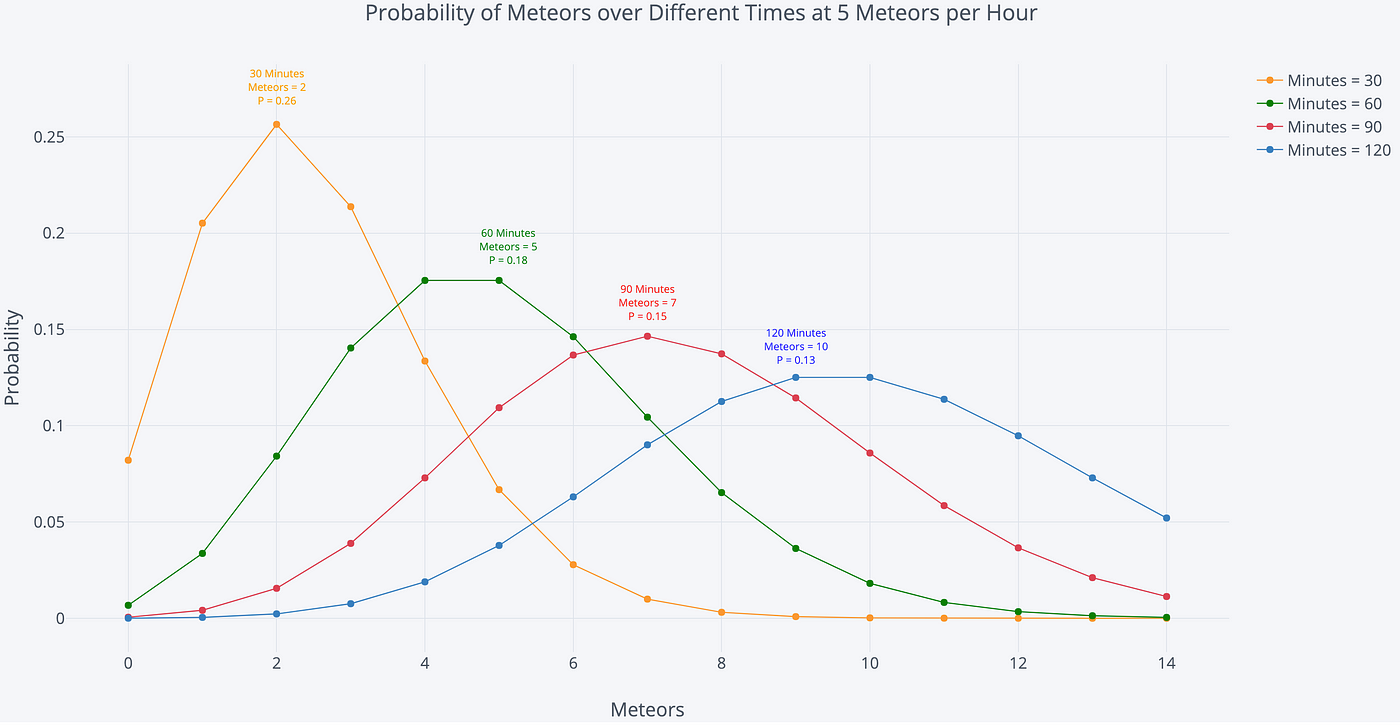
Information technology's no surprise that we expect to see more than meteors the longer we stay out! Whoever said "he who hesitates is lost" clearly never stood effectually watching meteor showers.
Waiting Fourth dimension
An intriguing part of a Poisson process involves figuring out how long we take to wait until the next issue (this is sometimes called the interarrival fourth dimension). Consider the situation: meteors appear once every 12 minutes on boilerplate. If we arrive at a random time, how long can nosotros expect to wait to see the next shooting star? My dad always (this time optimistically) claimed we simply had to look vi minutes for the first meteor which agrees with our intuition. Even so, if we've learned anything, it's that our intuition is not good at probability.
I won't get into the derivation (it comes from the probability mass function equation), but the time we tin await to wait between events is a decaying exponential. The probability of waiting a given corporeality of time between successive events decreases exponentially as the time increases. The following equation shows the probability of waiting more than a specified fourth dimension.
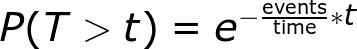
With our example, we take ane consequence/12 minutes, and if nosotros plug in the numbers we become a 60.65% chance of waiting > 6 minutes. So much for my dad'southward gauge! To show another example, we tin expect to wait more than than 30 minutes almost 8.2% of the fourth dimension. (We need to note this is between each successive pair of events. The waiting times between events are memoryless, then the fourth dimension between 2 events has no effect on the time betwixt whatsoever other events. This memorylessness is likewise known as the Markov property).
A graph helps united states of america to visualize the exponential decay of waiting time:
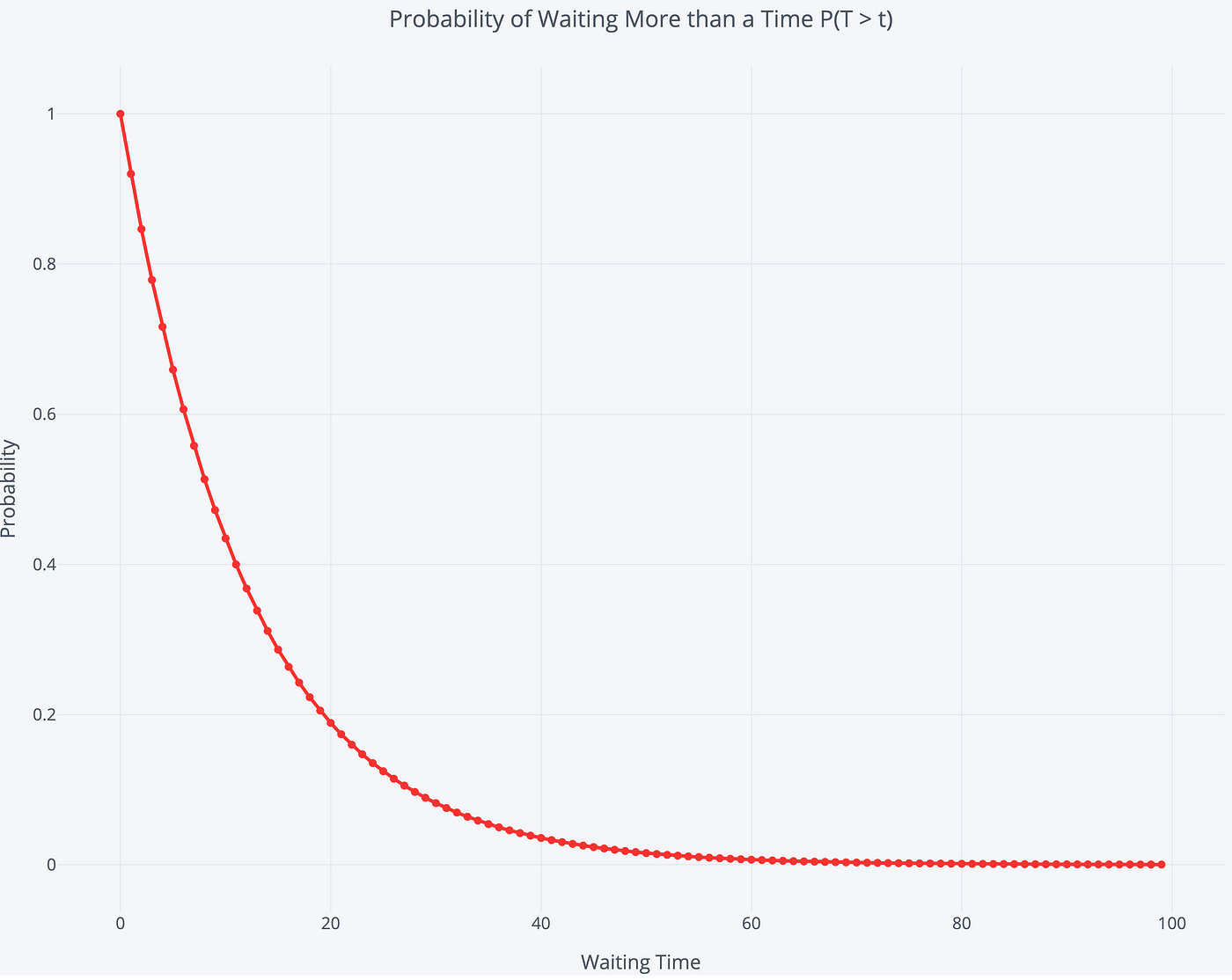
There is a 100% chance of waiting more than 0 minutes, which drops off to a near 0% run a risk of waiting more than 80 minutes. Again, since this is a distribution, in that location are a wide range of possible interarrival times.
Conversely, we can use this equation to find the probability of waiting less than or equal to a time:
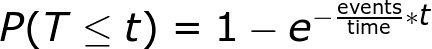
Nosotros can expect to wait 6 minutes or less to encounter a shooting star 39.4% of the fourth dimension. We tin can also find the probability of waiting a menstruation of time: in that location is a 57.72% probability of waiting between 5 and 30 minutes to see the next shooting star.
To visualize the distribution of waiting times, we tin can in one case once again run a (simulated) experiment. Nosotros simulate watching for 100,000 minutes with an boilerplate rate of 1 shooting star / 12 minutes. So, we find the waiting time between each meteor we run into and plot the distribution.
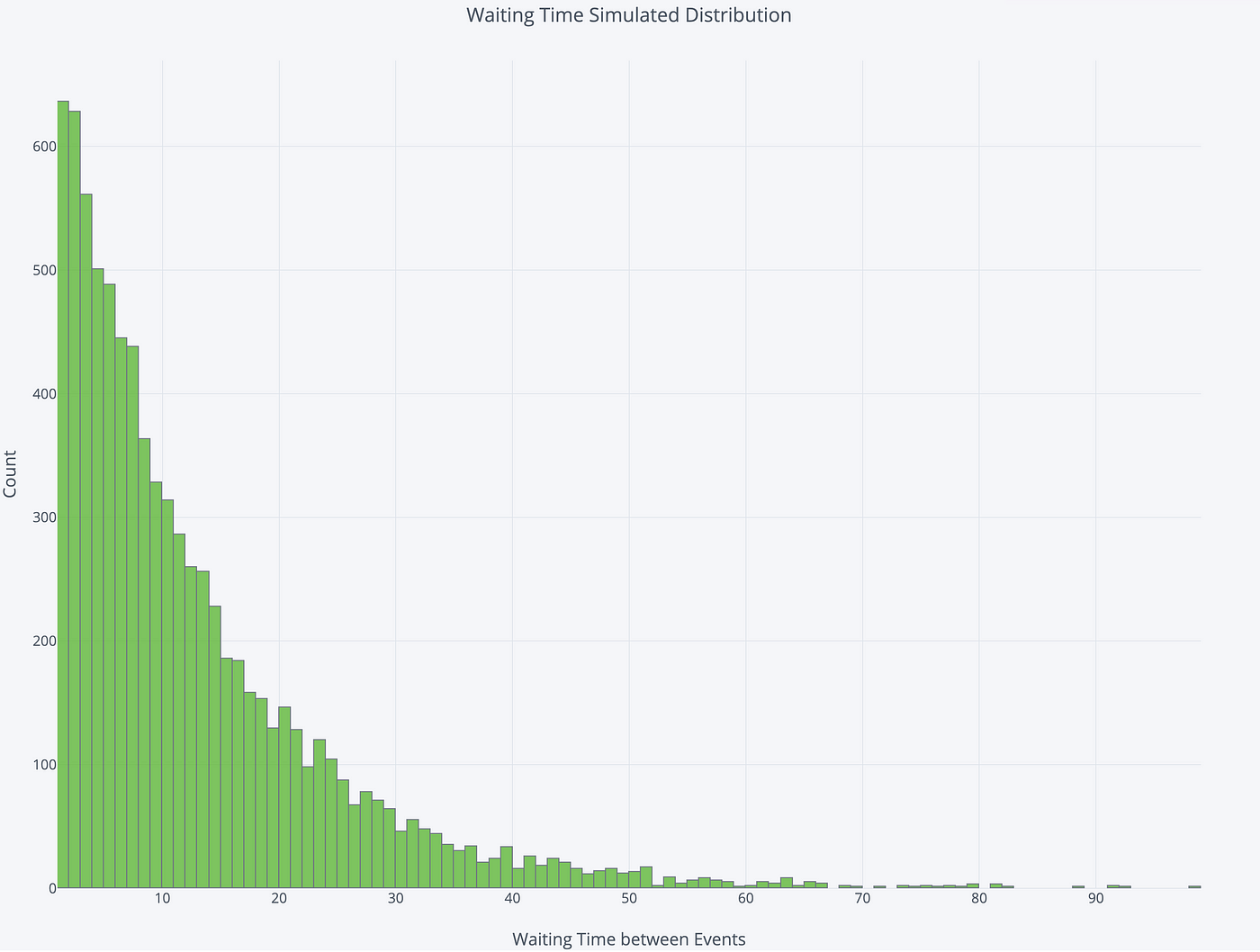
The nearly likely waiting time is ane minute, simply that is non the boilerplate waiting time. Permit's become back to the original question: how long tin we look to look on boilerplate to see the first shooting star if we get in at a random time?
To respond the boilerplate waiting time question, we'll run ten,000 dissever trials, each time watching the heaven for 100,000 minutes. The graph below shows the distribution of the average waiting fourth dimension between meteors from these trials:
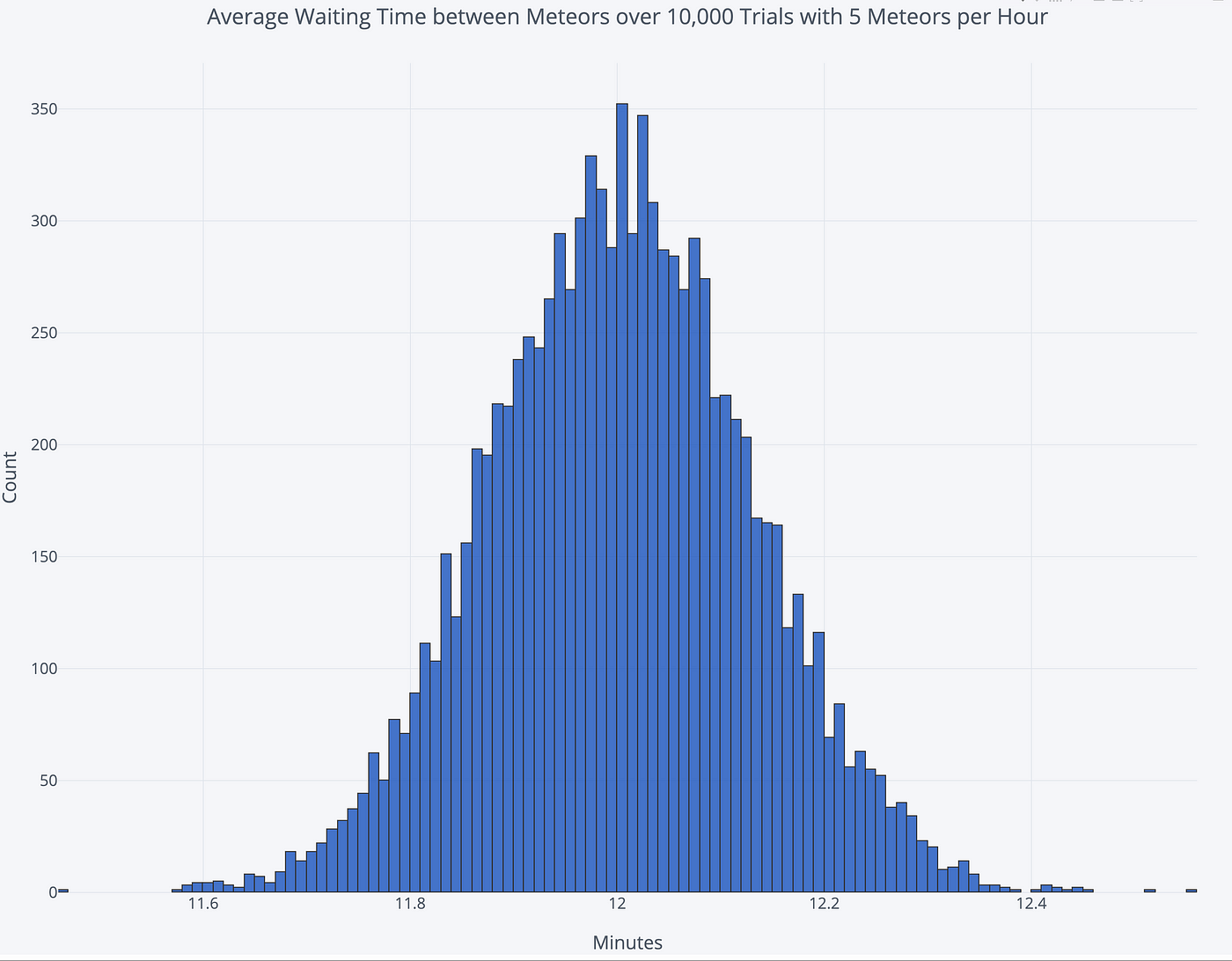
The average of the 10,000 averages turns out to exist 12.003 minutes. Even if nosotros arrive at a random time, the average time nosotros can look to expect for the first meteor is the average time between occurrences. At first, this may exist difficult to understand: if events occur on average every 12 minutes, then why should we take to await the unabridged 12 minutes before seeing 1 issue? The answer is this is an average waiting time, taking into business relationship all possible situations.
If the meteors came exactly every 12 minutes, then the average fourth dimension we'd accept to wait to see the first ane would be 6 minutes. However, considering this is an exponential distribution, sometimes we show up and have to expect an hour, which outweighs the greater number of times when nosotros wait fewer than 12 minutes. This is called the Waiting Time Paradox and is a worthwhile read.
As a final visualization, allow'south practise a random simulation of i hour of ascertainment.
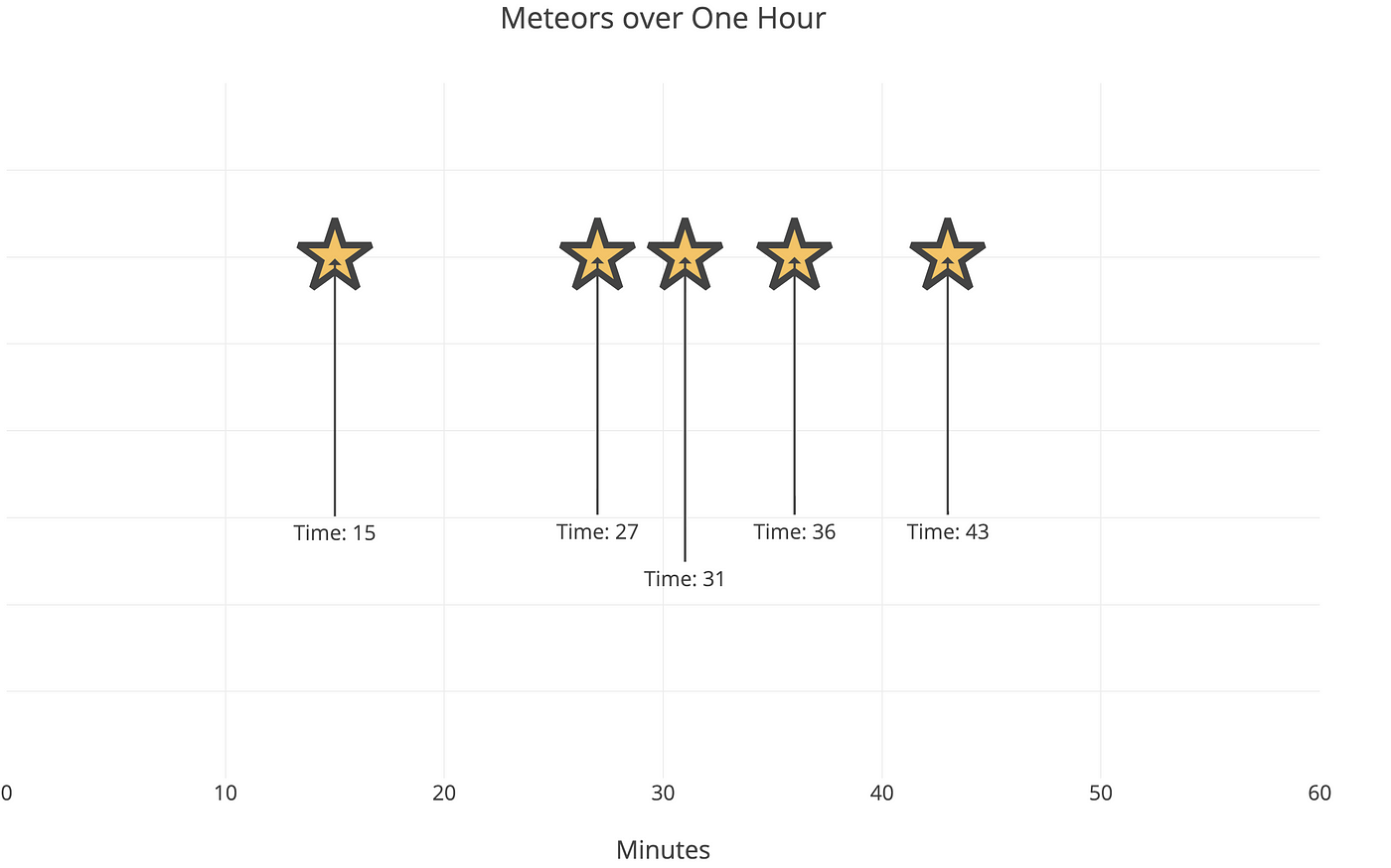
Well, this time we got exactly what we expected: 5 meteors. Nosotros had to wait 15 minutes for the first one, but and then had a proficient stretch of shooting stars. At least in this case, it'd be worth going out of the house for celestial observation!
Notes on Poisson Distribution and Binomial Distribution
A Binomial Distribution is used to model the probability of the number of successes nosotros can look from n trials with a probability p. The Poisson Distribution is a special case of the Binomial Distribution as n goes to infinity while the expected number of successes remains stock-still. The Poisson is used as an approximation of the Binomial if northward is large and p is small.
As with many ideas in statistics, "large" and "small" are up to interpretation. A rule of pollex is the Poisson distribution is a decent approximation of the Binomial if n > 20 and np < 10. Therefore, a money flip, fifty-fifty for 100 trials, should be modeled equally a Binomial because np =fifty. A call center which gets ane phone call every 30 minutes over 120 minutes could be modeled equally a Poisson distribution equally np = four. One important stardom is a Binomial occurs for a fixed set of trials (the domain is discrete) while a Poisson occurs over a theoretically space number of trials (continuous domain). This is only an approximation; remember, all models are wrong, but some are useful!
For more than on this topic, run across the Related Distribution section on Wikipedia for the Poisson Distribution. There is likewise a good Stack Exchange answer here.
Notes on Meteors/Meteorites/Meteoroids/Asteroids
Meteors are the streaks of lite you see in the heaven that are caused by pieces of debris called meteoroids burning upwards in the atmosphere. A meteoroid tin can come from an asteroid, a comet, or a piece of a planet and is unremarkably millimeters in diameter only can be upward to a kilometer. If the meteoroid survives its trip through the atmosphere and impacts Earth, it'southward called a meteorite. Asteroids are much larger chunks of rock orbiting the sun in the asteroid belt. Pieces of asteroids that break off become meteoroids. The more yous know!.
Conclusions
To summarize, a Poisson Distribution gives the probability of a number of events in an interval generated by a Poisson process. The Poisson distribution is divers by the rate parameter, λ, which is the expected number of events in the interval (events/interval * interval length) and the highest probability number of events. Nosotros can also employ the Poisson Distribution to find the waiting time between events. Even if nosotros arrive at a random fourth dimension, the boilerplate waiting time will always be the average time between events.
The next fourth dimension y'all find yourself losing focus in statistics, you lot have my permission to stop paying attending to the teacher. Instead, find the relevant equations and apply them to an interesting trouble. You lot can larn the material and yous'll have an appreciation for how stats helps us to sympathise the world. Above all, stay curious: there are many amazing miracle in the world, and we can use data science is a great tool for exploring them,
As always, I welcome feedback and effective criticism. I can be reached on Twitter @koehrsen_will.
Source: https://towardsdatascience.com/the-poisson-distribution-and-poisson-process-explained-4e2cb17d459
Post a Comment for "This Distribution Occurs Over and Over Again With Many Different Types of Data"